Perhatikan gambar di samping!
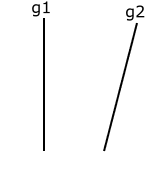
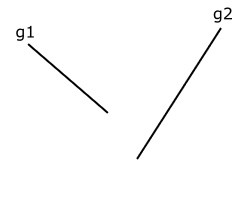
Apakah garis-garis yang terdapat pada gambar 1 disamping saling berpotongan?
Kesimpulan
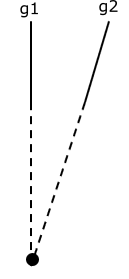
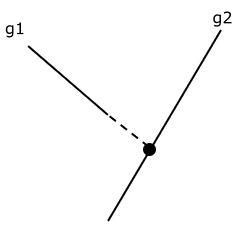
Dua buah garis yang tidak sejajar dan terletak pada bidang datar akan saling berpotongan disebuah titik. Agar kedua garis berpotongan maka kedua garis diperpanjang (lihat gambar 2). Ketiga garis tersebut memiliki satu titik potong.
Bagaimana cara menentukan titik potong sebuah persamaan?
Pembahasan
Apabila g1 dan g2 adalah dua buah garis yang tidak sejajar dengan persamaan y=a1x+b1 dan y=a2x+b2 maka titik potong kedua garis tersebut adalah sebuah titik yang terletak pada kedua garis dan memenuhi persamaan a1x+b1=a2x+b2.
Maka:
Titik potong dua garis yang tidak sejajar dengan persamaan y=a1x+b1 dan y=a2x+b2 dapat diperoleh dengan menyelesaikan persamaan a1x+b1=a2x+b2
Agar lebih memahami rumus diatas, kerjakan contoh soal dibawah ini dengan jawaban yang benar!
Kegiatan Siswa
Tentukan titik potong dari garis y=4x−1 dan y=x+8!
Kegiatan Siswa
Petunjuk: Isilah kotak kosong di bawah ini dengan jawaban yang benar!
Masukkan kedua persamaan kedalam rumus a1x+b1=a2x+b2
- = +
- = +
=
| = | ||
x =
Nilai y diperoleh dengan cara memasukkan nilai x dari hasil diatas ke salah satu persamaan, kita ambil persamaan y=4x−1
y=4 - 1
y = - 1
y=
Kesimpulan
Jadi, titik potong kedua garis tersebut adalah (3, 11).
Gambar
 |
 |
 |
Gambar 1. Garis-garis tidak sejajar
 |
 |
 |
Gambar 2. Garis-garis tidak sejajar
