 |
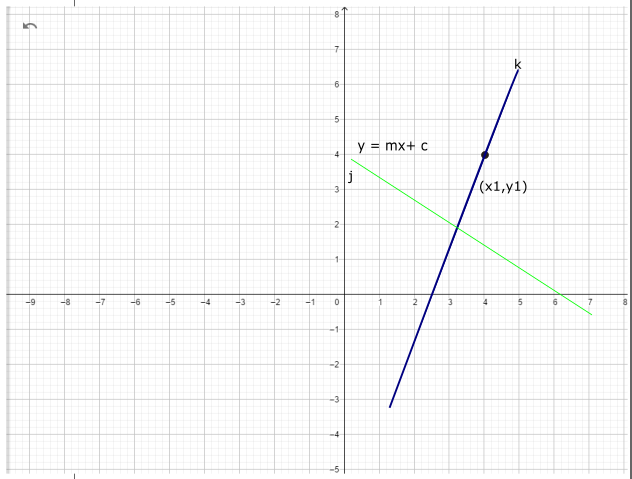
Perhatikan gambar di atas, garis j dan garis k saling tegak lurus. Persamaan garis j adalah y = mx + c dan garis k melalui titik ${(x_1, y_1)}$
Persamaan garis yang melalui titik ${(x_1,y_1)}$ dan tegak lurus dengan garis ${y = mx + c}$ adalah $y - {y_1}$ = - $\frac{1}{m}$ ${(x - x_1)}$ Ket: -1 didapatkan dari rumus ${m_1}$ x ${m_2}$ = -1
Agar lebih memahami rumus di atas, kerjakan contoh soal disamping dengan benar!
Persamaan Garis yang Melalui Titik ${(x_1,y_1)}$ dan ${(x_2,y_2)}$
Pada materi sebelumnya telah diketahui rumus umum untuk mencari gradien garis yang melalui titik ${(x_1,y_1)}$ dan ${(x_2,y_2)}$ adalah $m = \frac{y_2-y_1}{x_2-x_1}$ atau $m = \frac{y_1-y_2}{x_1-x_2}$. Maka untuk menentukan persamaan garis yang melalaui titik ${(x_1,y_1)}$ dan ${(x_2,y_2)}$ dapat menggunakan rumus persamaan garis dengan mensubstitusikan rumus $m = \frac{y_2-y_1}{x_2-x_1}$ ke dalam rumus persamaan ${y - y_1} = {m (x-x_1)}$
Kegiatan Siswa
Untuk mendapatkan rumus umum gradien garis yang melalui titik ${(x_1,y_1)}$ dan ${(x_2,y_2)}$, kerjakan soal di bawah ini dengan teliti!
Lengkapi kotak yang kosong dibawah ini agar mendapatkan rumus yang benar!
Penyelesaian
ganti m yang terdapat pada persamaan ${y - y_1} = {m (x-x_1)}$ dengan $\frac{y_1-y_2}{x_1-x_2}$
| ${y - y_1}$ | = | $\Bigg($ | - | $\Bigg)$ | ${(x - x_1)}$ |
| - |
| ${y - y_1}$ | = | - ${(x - x_1)}$ | |
| - |
ruas kanan dan ruas kiri dibagi dengan ${(y_1,y_2)}$
| ${y - y_1}$ | = | ( - )${(x - x_1)}$ | |
| - | ( - )( - ) |
| ${y - y_1}$ | = | ${(x - x_1)}$ |
| - | - |
Kesimpulan
Jadi, rumus untuk menentukan persamaan garis yang melalui titik ${(x_1,y_1)}$ dan ${(x_2,y_2)}$ adalah
$\frac{y - y_1}{y_1 - y_2}$ = $\frac{x - x_1}{x_1 - x_2}$
Contoh
Kegiatan Siswa
Tentukan persamaan garis yang melalui titik (1,3) dan tegak lurus dengan garis y = - $\frac{1}{2}$x - 4
Penyelesaian
Petunjuk: Isilah kotak kosong di bawah ini dengan jawaban yang benar!
Diketahui nilai m = , ${x_1}$ = , ${y_1}$ =
Kemudian masukkan kedalam persamaan y - ${y_1}$ = m${(x - x_1)}$
Akan diperoleh:
y - = (x - )
y - = x -
y = x - +
y = x +
Diketahui: m = 2, ${x_1}$ = 1, ${y_1}$ = 3
Gradien garis y = -$\frac{1}{2}x$- 4 adalah -$\frac{1}{2}$, karena tegak lurus maka persamaan garis yang melalui titik (1,3) bergradien 2.
y - ${y_1}$ = m (x - ${x_1}$)
y - 3 = 2 (x - 1)
y - 3 = 2x + 2
y = 2x + 2 + 3
y = 2x + 1
Jadi, persamaan garis yang melalui titik (1,3) dan tegak lurus dengan garis y = -$\frac{1}{2}x$- 4 adalah y = 2x + 1
Kegiatan Siswa
Tentukan persamaan garis yang melalui titik P(3,2) dan Q(-1,0)
Penyelesaian
Petunjuk: Isilah kotak kosong di bawah ini dengan jawaban yang benar!
Tentukan nilai ${x_1}$ = dan ${y_1}$ = dari titik P
Tentukan nilai ${x_2}$ = dan ${y_2}$ = dari titik Q
Masukkan kedalam rumus $\frac{y - y_1}{y_1 - y_2}$ = $\frac{x - x_1}{x_1 - x_2}$
| y - | = | x - |
| - | - |
| y - | = | x - |
| + |
| y - | = | x - |
Kali silang kedua ruas
(y - ) = (x - )
y - = x -
y = x - +
y = x +
| y | = | (2x + 2) | |
| y | = | (x + 1) | |
Kesimpulan
Jadi,persamaan garis yang melalui titik P(3,2) dan Q(-1,0) adalah y = $\frac{1}{2} x$+ 1
