Tujuan Pembelajaran
- Siswa dapat menentukan :
- Persamaan garis bergradien m dan melalui titik (x1,y1)
- Persamaan garis melalui sebuah titik dan sejajar garis lain
- Persamaan garis melalui sebuah titik dan tegak lurus garis lain
- Persamaan garis melalui dua titik (x1,y1)
- Koordinat titik potong dua garis
- Siswa dapat memahami penerapan konsep persamaan garis lurus dalam kehidupan sehari-hari
Persamaan Garis Bergradien m dan Melalui Titik (x1,y1)
Bagaimana kita bisa menentukan persamaan garis lurus jika yang diketahui gradien dan salah satu titik yang di lalui garis lurus tersebut?
Untuk menjawab pertanyaan di atas, lengkapi jawaban di bawah ini dengan benar!
Rumus umum sebuah persamaan adalah y = mx + c. Jika diketahui gradien m dan melalui titik (x1,y1), maka akan diperoleh persamaan:
y1 = mx1 + c atau c = y1 - mx1
Dengan mensubstitusikan c = y1 - mx1 ke dalam persamaan y = mx + c, maka bentuk persamaannya kan menjadi:
y = mx + -
y - = mx -
y - = m( - )
Kesimpulan
Jadi, dari penyelesaian diatas dapat kita simpulkan bahwa Persamaan garis yang memiliki gradien m dan melalui titik (x1,y1) adalah y−y1 = m(x−x1)
Persamaan Garis Melalui Sebuah Titik dan Sejajar Garis Lain
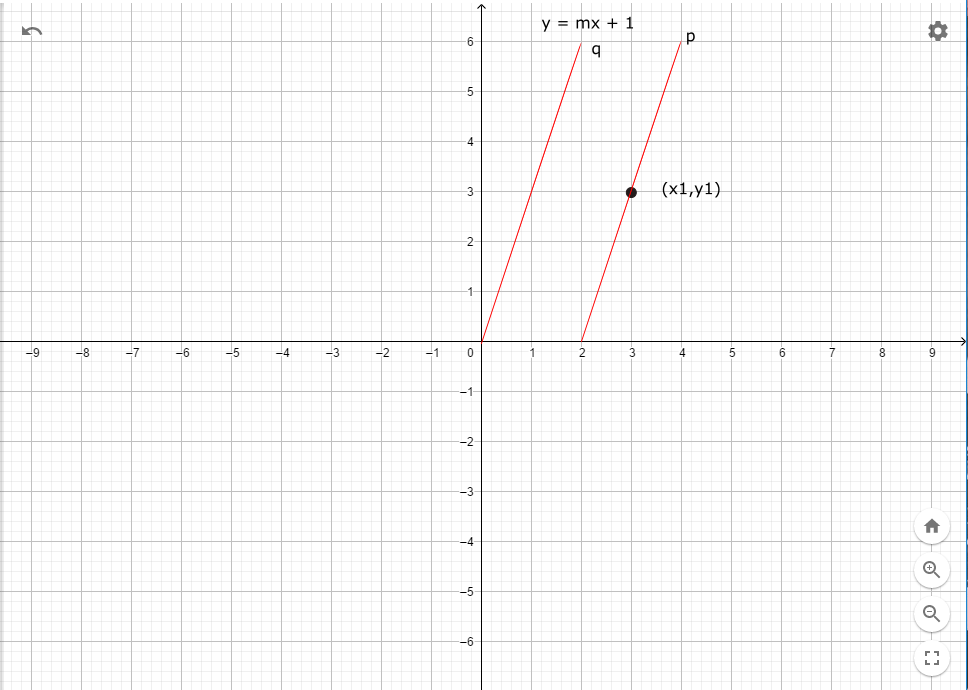 |
Perhatikan gambar di atas, garis p dan q sejajar dimana persamaan garis q adalah y = mx + c. Sedangkan garis p melewati titik (x1,y1). Karena garis p dan q saling sejajar maka kedua garis tersebut memiliki gradien yang sama (mp=mq=m)
Maka dapat disimpulkan persamaan garis yang melalui titik (x1,y1) dan sejajar dengan garis p adalah y−y1 = m(x−x1)
Agar lebih memahami, kerjakanlah contoh soal disamping dengan benar.
Contoh soal
Kegiatan Siswa
Tentukan persamaan garis jika diketahui gradiennya adalah 3 dan melalui titik (-2,1)!
Penyelesaian
Petunjuk: Isilah kotak kosong di bawah ini dengan jawaban yang benar!
Diketahui nilai m = , x1 = , y1 =
Kemudian masukkan kedalam persamaan y - y1 = m(x−x1)
Akan kita peroleh
y - = (x - ())
y - = (x + )
y - = x +
y = x + +
y = x +
Kesimpulan
Jadi,garis yang memiliki gradien 3 dan melalui titik (-2,1) adalah y = 3x + 7
Aktivitas Siswa
Tentukan persamaan garis yang melalui titik (-3,5) dan sejajar dengan garis y = 4x + 8!
Penyelesaian
Petunjuk: Isilah kotak kosong di bawah ini dengan jawaban yang benar!
Diketahui m = , x1 = , y1 = , kemudian masukkan sesuai rumus y - y1 = m(x−x1)
y - = (x - ())
y - = (x + )
y - = x +
y = x + +
y = x +
Kesimpulan
Jadi,persamaan garis yang melewati titik (-3, 5) dan sejejar dengan garis y = 4x + 8 adalah y = 4x + 17
