Untuk menyelesaikan gradien garis yang melalui dua titik, kita harus menghitung nilai perbandingan komponen x dan komponen y. Agar lebih memahami gradien garis yang melalui dua titik, perhatikan gambar 7 disamping.
Garis f dengan persamaan y = 2x + 1 melalui titik D (0,1),
E (-1,-1), F (2,5), dan G (3,7)

Aktivitas Siswa
Amati Gambar 7. persamaan y = 2x + 1 disamping dan lengkapi tabel di bawah ini dengan benar!
Penyelesaian
Petunjuk : Isilah kotak kosong di bawah ini dengan jawaban yang benar!
Tabel perbandingan komponen x dan komponen y
Persamaan y = 2x + 1
| Garis DE | Garis EF | Garis FG | |
|---|---|---|---|
| Komponen x | xE-xD = -1 - 0 = -1 | ||
| Komponen y | yE-yD = -1 - 1 = -2 | ||
| $\frac{Komponen y}{Komponen x}$ | $\frac{y_E - y_D}{x_E - x_D} =\frac{-2}{-1}$ = 2 |
Penyelesaian
Komponen x pada ruas garis EF = 3 dan komponen y pada ruas garis EF = 6
$\frac{Komponen y}{Komponen x}$ = $\frac{6}{3}$
Komponen x pada ruas garis FG = 1 dan komponen y pada ruas garis FG = 2
$\frac{Komponen y}{Komponen x}$ = $\frac{2}{1}$
Kegiatan Siswa
Perhatikan Gambar 8 disamping dan lengkapilah tabel dibawah ini dengan benar!
Penyelesaian
Petunjuk : Isilah kotak kosong di bawah ini dengan jawaban yang benar!
Tabel perbandingan komponen x dan komponen y
Persamaan Garis y = -2x + 2
| Garis AB | Garis BC | Garis CD | |
|---|---|---|---|
| Komponen x | |||
| Komponen y | |||
| $\frac{Komponen y}{Komponen x}$ |
Ket: Jika kotak berwarna Hijau maka jawaban Benar
Jika kotak berwarna Merah maka jawaban salah
Kesimpulan
Dari kedua tabel di atas perbandingan komponen y dan komponen x mempunyai nilai yang sama atau tetap disetiap ruas garis. Nilai perbandingan itulah yang disebut gradien atau kemiringan suatu garis. Jadi, persamaan garis y = 2x + 2 mempunyai gradien 2 dan persamaan garis
y = -2x + 2 mempunyai gradien -2.
Rumus
Dari contoh soal diatas dapat diperoleh rumus umum dengan ketentuan sebagai berikut:
Jika yE = y2, Jika yD = y1, Jika xE = x2, Jika yD = x1
Maka rumus umumnya adalah:
| m | = | - |
| - |
catatan: tuliskan jawaban dengan huruf kecil
Gambar
grafik persamaan y = 2x + 1
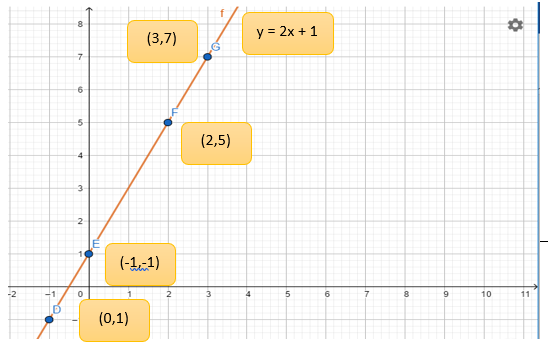 |
Gambar 7
grafik persamaan y = -2x + 2
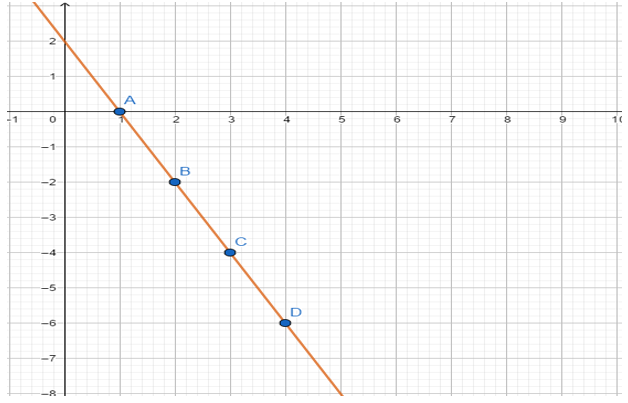 |
Gambar 8
